"""
Aleksandar Milkovic
"""
|
|
# Sustavi nelinearnih jednadžbi
|
|
# 1. Rješavanje simbolički korištenjem funkcije solve(); u praksi jedino radi nad jednostavnim sustavima !
|
|
var('x y z')
(x, y, z) |
eq1 = x^2+y^2==11
|
|
eq2 = sqrt(x)-y^3==13
|
|
solve([eq1,eq2],[x,y])
[[x == 2.43369890329, y == -2.25324419976], [x == (-3.70557044938 - 0.678918482901*I), y == (1.27470173064 - 1.97362269722*I)], [x == (3.72178172825 - 0.574750273542*I), y == (1.1055676034 + 1.93483877403*I)], [x == (3.72178172825 + 0.574750273542*I), y == (1.1055676034 - 1.93483877403*I)], [x == (-3.70557044938 + 0.678918482901*I), y == (1.27470173064 + 1.97362269722*I)]] |
sol = solve([eq1,eq2],[x,y], solution_dict=True)
|
|
[[s[x].n(24),s[y].n(24)] for s in sol] # ispisuje sve parove rješenja
[[2.43370, -2.25324], [-3.70557 - 0.678918*I, 1.27470 - 1.97362*I], [3.72178 - 0.574750*I, 1.10557 + 1.93484*I], [3.72178 + 0.574750*I, 1.10557 - 1.93484*I], [-3.70557 + 0.678918*I, 1.27470 + 1.97362*I]] |
[s[x] for s in sol] # ispisuje samo rješenja x-a
[2.43369890329, -3.70557044938 - 0.678918482901*I, 3.72178172825 - 0.574750273542*I, 3.72178172825 + 0.574750273542*I, -3.70557044938 + 0.678918482901*I] |
# 2. Numeričko rješavanje
|
|
# 1. primjer
|
|
jd1 = sin(x)+cos(y)==1
|
|
jd2 = x^2-y^2==1
|
|
solve([jd1,jd2],x,y) # vidimo da ne daje rješenje
[x^2 - y^2 == 1, sin(x) + cos(y) == 1] |
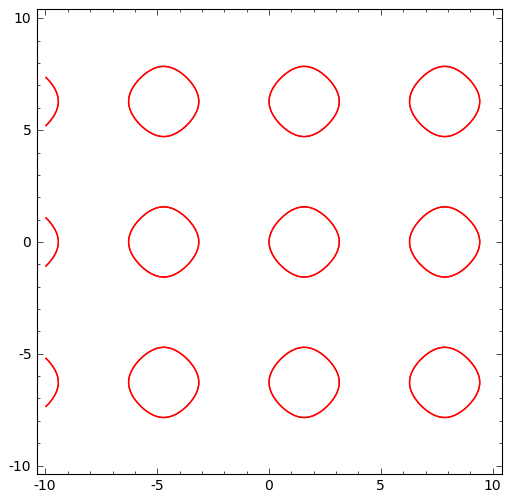
f(x,y) = sin(x)+cos(y)-1==0
|
|
implicit_plot(f,(x,-10,10),(y,-10,10),color="red").show(aspect_ratio=1) # funkcija implicit_plot crta implicitno zadanu funkciju
|
|
g(x,y) = x^2-y^2-1==0
|
|
implicit_plot(g,(x,-10,10),(y,-10,10),color="red")
|
|
h(x,y) = f(x,y)^2+g(x,y)^2
|
|
h
(x, y) |--> (sin(x) + cos(y) - 1)^2 + (x^2 - y^2 - 1)^2 == 0 |
m = minimize(h,[.1,.2], disp=0) # disp=0 služi kako minimize ne bi prikazo inače prikazive informacij o optimizacijskom procesu
|
|
m1 = m[0]; m2 = m[1]
|
|
m1,m2
(1.83328733261, -1.53653593604) |
# provjera rezultata
|
|
h(m1,m2)
(1.35554783078e-13) == 0 |
f(m1,m2)
(2.8019153659e-07) == 0 |
g(m1,m2)
(-2.38846155298e-07) == 0 |
m1^2-m2^2
0.999999761154 |
sin(m1)+cos(m2)
1.00000028019 |
# 2. primjer
|
|
a1 = 2*x-y-6*ln(y)-3==0
|
|
a2 = 15*x-10*y-60*ln(y)-6==0
|
|
#solve([a1,a2],[x,y]) #kada bi ovo probali izračunati worksheet bi se smrznuo
|
|
t1(x,y) = a1
|
|
implicit_plot(t1,(x,-10,10),(y,0,10))
|
|
t2(x,y) = a2
|
|
implicit_plot(t2,(x,-10,10),(y,0,10))
|
|
t(x,y) = t1(x,y)^2+t2(x,y)^2
|
|
t
(x, y) |--> (2*x - y - 6*log(y) - 3)^2 + (15*x - 10*y - 60*log(y) - 6)^2 == 0 |
n = minimize(t,[.1,.2]) # ovdje vidimo da bez disp=0 Sage ispisiju informacije o optimizacijskom procesu
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 43
Function evaluations: 50
Gradient evaluations: 50
|
n1 = n[0]; n2 = n[1]
|
|
n1,n2
(4.8000000216, 2.11256967106) |
# provjera
|
|
t(n1,n2)
(2.02350929876e-16) == 0 |
t1(n1,n2)
(1.16220251201e-08) == 0 |
t2(n1,n2)
(8.20240586563e-09) == 0 |
# osim gore navedene metode numeričkog računanja (koja je vrlo jednostavna i shvatljiva), mogu se primjeniti i
# neke od metoda koje smo naučili ranije na Numeričkoj matematici poput Newtnove, itd..
|
|

.png)
.png)
.png)